AC Circuits

Electrician Trade Theory, Module-6

Posted May 29, 2025 Updated May 29, 2025

By Roni

10 min read

AC Circuits

⭕️ Show all Answers

Q1: What is the unit of susceptance?

Mho
Ohm
Henry
Farad

Q2: What is the resistance of the inductive coil takes 5A current across 240V, 50Hz supply at 0.8 power factor?

48 \(\Omega\)
42.5 \(\Omega\)
38.4 \(\Omega\)
26.6 \(\Omega\)

Show Calculation

Given:
\[ V = 240\,\text{V}, I = 5\text{A},\cos\theta = 0.8\]\[ Real Power~ P = VI \cos\theta\]\[ = 240 \times 5 \times 0.8 = 960\,\text{W}\]\[ Resistance ~R = \frac{P}{I^2} = \frac{960}{5^2} = \frac{960}{25} = 38.4\,\Omega\]

Q3: How the resonance frequency \((f_r)\) can be increased in A.C series circuit?

Increasing the inductance value
Reducing the capacitance value
Increasing the capacitance value
Increasing the value of resistance

Q4: What is the formula to find 3 phase Reactive power \((P_R)\) if the line voltage is \(V_L\) and line current is \(I_L\)?

\(P_r\) = \(V_L\) \(I_L\)
\(P_r = \sqrt{3} V_L\) \(I_L\) cosθ
\(P_r = \sqrt{3} V_L\) \(I_L\)
\(P_r\) = \(V_L\) \(I_L\) sinθ

Q5: What is the main cause for below 0.5 lagging power factor in 3 phase system?

Due to fluctuation of voltage
True power due to resistive load
Reactive power due to more inductive load
Reactive power due to more capacitive load

Q6: What is the current in neutral conductor in 3 phase unbalanced load in star connected system?

No current will flow
The algebraic sum of current in 3 phases
The algebraic sum of current in 2 phases only
Lesser than the lowest current in any one of the phases

Q7: Calculate the apparent power in KVA of 3 phase 415V, 50 Hz, star system, if the line current \((I_L)\) is 16A at 0.8 power factor.

15.2 KVA
11.5 KVA
9.2 KVA
5.3 KVA

Show Calculation

Given:
\[Line ~Voltage ~V_L = 415\,\text{V}, Current ~I_L = 16\,\text{A}\]\[ Power~ Factor ~\cos\theta = 0.8\] \[Apparent ~Power ~S = \sqrt{3} V_L I_L \]\[= \sqrt{3} \times 415 \times 16 \approx 1.732 \times 415 \times 16\]\[ = 11487.68\,\text{VA} = 11.5\,\text{KVA}\]

Q8: What will be the readings of two watt meters \((W_1\) & \(W_2)\) in 3 phase power measurement, if the power factor is zero?

\((W_1\) & \(W_2)\) both are positive reading
\(W_1\) is Positive and \(W_2\) is negative reading
\(W_1\) is equal to \(W_2\) but with opposite signs
Zero \(W_1\) is Positive reading, and \(W_2\) is negative reading

Q9: What is the maximum value of voltage for 240 volt RMS?

240V
415V
339.5V
376.8V

Show Calculation

Given: RMS Voltage \(V_{rms} = 240\,\text{V}\)

Maximum Voltage \(V_{max} = \sqrt{2} \times V_{rms} = \sqrt{2} \times 240\) \[\approx 1.414 \times 240 = 339.36\,\text{V}\]

Q10: What is the condition for resonance in RLC series circuit? (Inductive reactance = \(X_L\), Capacitive reactance = \(X_C\))

\(X_L\) > \(X_C\)
\(X_L\) < \(X_C\)
\(X_L\) = \(X_C\)
\(X_L\) > \(\sqrt{2} X_C\)

Q11: What is the formula for Reactive Power \((P_r)\) in an AC circuit?

\(P_r\) = VI
\(P_r\) = \(\sqrt{2}\) VI
\(P_r\) = VI cosθ
\(P_r\) = VI sinθ

Q12: Calculate the impedance of the circuit R = 5Ω, \(X_L\)= 36Ω and \(X_C\) = 24 Ω.

69 Ω
65 Ω
13 Ω
12 Ω

Show Explanation

Given: \(R = 5\,\Omega\), \(X_L = 36\,\Omega\), \(X_C = 24\,\Omega\)

Net Reactance \(X = X_L - X_C = 36 - 24 = 12\,\Omega\)

\[Impedance ~Z = \sqrt{R^2 + X^2} \]= \(\sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13\,\Omega\)

Q13: What is the phase displacement in a single phase AC circuit?

90°
120°
180°
270°

Q14: What is the relation between the line voltage \((V_L)\) and phase voltage \((V_p)\) in star connected system?

\(V_L = \sqrt{3} V_P\)
\(V_L = 3 V_P\)
\(V_L = V_P\)
\(V_L = \frac {V_P}{\sqrt{3}}\)

Q15: Calculate the line current of the 3 phase 415V 50 HZ supply for the balanced load of 3000 watt at 0.8 power factor is connected in star.

8.5 A
5.2 A
4.5 A
3.4 A

Show Explanation

\[ Given: P = 3000\,\text{W}, V_L = 415\,\text{V}, \cos\theta = 0.8\] \[I_L = \frac{P}{\sqrt{3} \times V_L \times \cos\theta}\]\[ = \frac{3000}{\sqrt{3} \times 415 \times 0.8} \approx \frac{3000}{574.28} = 5.22\,\text{A}\]

Q16: What is the power factor in a 3 phase power measurement of two wattmeters showing equal readings?

Q17: Calculate the power factor of coil having resistance of 24Ω, draws the current of 5A, at 240V/ 50Hz AC supply.

Show Calculation

\[ Given: R = 24\,\Omega, I = 5\,\text{A}, V = 240\,\text{V}\] \[ Apparent ~Power S = VI = 240 \times 5 = 1200\ \text{VA}\] \[ Real Power ~P = I^2 R = 5^2 \times 24\]\[ = 25 \times 24 = 600\,\text{W}\] \[ \cos\theta = \frac{P}{S} = \frac{600}{1200} = 0.5\]

Q18: What is the formula to calculate the impedance (Z) of the R.L.C series circuit, if the inductive reactance \((X_L)\) is less than capacitive reactance \((X_C)\)?

\(Z = \sqrt{R^2 + X_L^2 + X_C^2}\)
\(Z = \sqrt{R^2 + (X_C - X_L)^2}\)
\(Z = \sqrt{R^2 + (X_L - X_C)^2}\)
\(Z = R + X_L + X_C\)

Q19: Calculate the power factor of R.L.C circuit having resistance (R) = 15Ω, resultant reactance (X) = 20Ω connected across 240V /50Hz AC supply?

Show Calculation

\[ Given: R = 15\,\Omega, X = 20\,\Omega\] \[Impedance Z = \sqrt{R^2 + X^2} = \sqrt{15^2 + 20^2} \]\[ = \sqrt{225 + 400} = \sqrt{625} = 25\,\Omega\] \[\cos\theta = \frac{R}{Z} = \frac{15}{25} = 0.6\]

Q20: Calculate the value admittance (Y) of the RLC parallel circuit connected across 240volts/50Hz AC supply and 8 Amp. Current is passed through it?

3.33 Mho
0.33 Mho
0.033 Mho
0.003 Mho

Show Calculation

\[ Given: V = 240 \text{V}, I = 8 \text{A}\] \[Admittance ~Y = \frac{I}{V} = \frac{8}{240} = 0.0333\,\text{Mho}\]

Q21: What is the formula to calculate the line current \((I_L)\) of this single phase R - C parallel circuit?

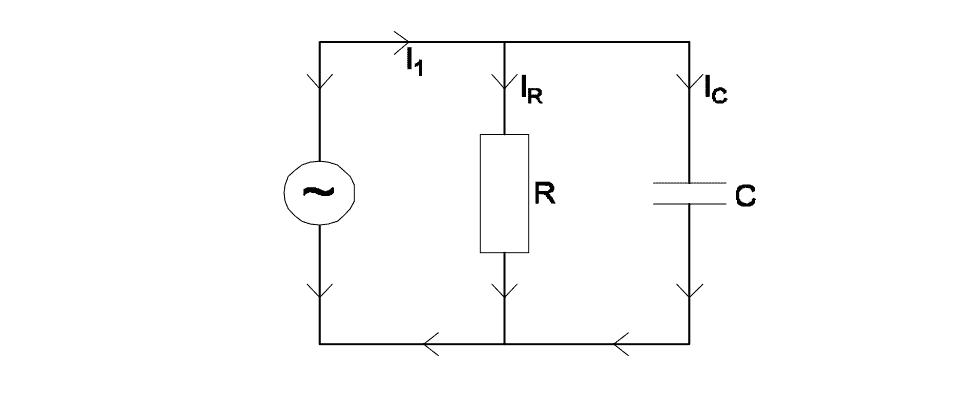
\(I_L = I_R - I_C\)
\(I_L = I_R + I_C\)
\(I_L = \sqrt{I_R^2 + I_C^2}\)
\(I_L = \sqrt{I_C^2 + I_{RL}^2}\)

Q22: How the low power factor (P.F) can be improved in AC circuits?

By connecting resistors in series
By connecting capacitors in series
By connecting inductors in series
By connecting capacitors in parallel

Q23: What is the formula to calculate the three phase active power (P) if the line voltage (VL) and line current is \(I_L\) and phase angle is ‘θ’?

\(P = \sqrt{3} V_L I_L \sin\theta\)
\(P = \sqrt{3} V_L I_L\)
\(P = \sqrt{3} V_L I_L \cos\theta\)
\(P = V_L I_L \sin\theta\)

Q24: What is the relation between the line current \((I_L)\) and phase current \((I_P)\) in delta connected system?

\(I_L = I_P\)
\(I_L = 3 I_P\)
\(I_L = \sqrt 3 I_P\)
\(I_L = \frac{I_P} {\sqrt 3}\)

Q25: What is the purpose of phase sequence meter?

To control the speed of 3 phase motor
To protect motor against short circuit fault
To indicate the incorrect phase sequence of 3 phase
To ensure the correct phase sequence of 3 phase system

Q26: Calculate the apparent power of a star connected 3 phase load, if it is connected across 3 phase 415volt/50Hz supply at 0.8 p.f and the phase current is 10 Amps.

12.45 KVA
57.50 KVA
3.320 KVA
7.188 KVA

Show Calculation

\[ Given: V_L = 415\,\text{V}, I_P = 10\,\text{A}, Star system\] \[Line ~current~ in ~star = Phase~ current = 10 \text{A}\] \[ Apparent ~Power ~S = \sqrt{3} V_L I_L \]\[= \sqrt{3} \times 415 \times 10 = 7188.8\,\text{VA} = 7.188\,\text{KVA}\]

Q27: What is the P.F if one of the wattmeters reading is zero and the other reads total power in 2 wattmeter method of 3 phase power measurement?

0.5
Zero
Unity
Below 0.5

Q28: Which electrical term is defined as the total opposition to current in AC parallel circuit?

Resistance
Impedance
Admittance
Susceptance

Q29: Which AC circuit contains the phase relation between voltage (V) and current (I)?

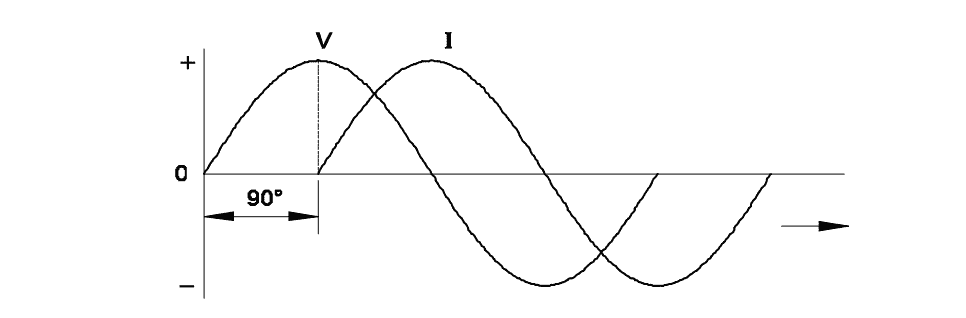
Pure resistive circuit
Resistance and inductance circuit
Resistance and capacitance circuit
Resistance, inductance and capacitance circuit

Q30: In a 3 phase system, if the active power is 4 kw and the apparent power is 5 KVA, calculate the reactive power?

1 KVAR
2 KVAR
3 KVAR
4 KVAR

Show Calculation

\[ Given: P = 4\,\text{KW}, S = 5\,\text{KVA}\] \[ Reactive Power Q = \sqrt{S^2 - P^2} = \sqrt{5^2 - 4^2} \]\[= \sqrt{25 - 16} = \sqrt{9} = 3\,\text{KVAR}\]

Q31: In which condition resonance will occur in R-L-C series circuit?

Inductive reactance \((X_L)\) is zero
Inductive reactance \((X_L)\) is equal to capacitive reactance \((X_C)\)
Inductive reactance \((X_L)\) is greater than capacitive reactance \((X_C)\)
Inductive reactance \((X_L)\) is less than capacitive reactance \((X_C)\)

Q32: How will you obtain positive reading in the wattmeter reads negative reading during 3-phase two wattmeter method?

By interchanging the connections of input terminals
By disconnecting the connection of current coil in meter
By reversing the connection of pressure coil in meter
By reversing the pressure coil and current coil connection in meter

Q33: What is the form factor \((K_f)\) for sinusoidal AC?

1.00
1.11
2.22
4.44

Q34: What is the reciprocal of inductance in AC parallel circuit?

Reactance
Admittance
Conductance
Susceptance

Q35: What relationship is illustrated in between the current and voltage?

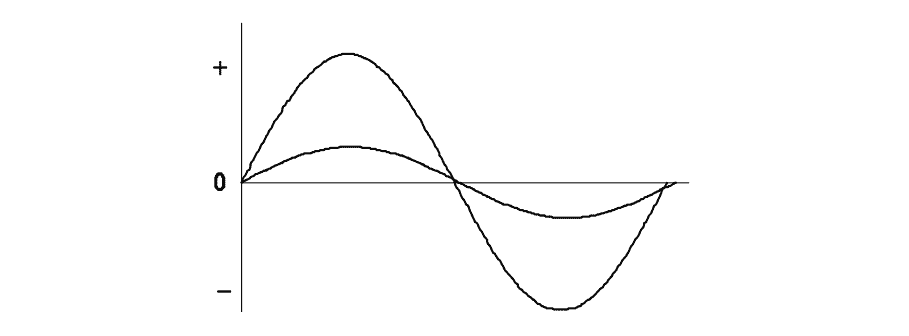
Current and voltage are “in phase”
Current and voltage are in out of phase
Current lags behind the voltage
Current leads ahead of the voltage

Q36: Calculate the total power by two wattmeter \((W_1\) & \(W_2)\) method, if one of the wattmeter \((W_2)\) reading is taken after reversing.

\(W_1\) x 2
\(W_1 only\)
\(W_1 - W_2\)
\(W_1 + W_2\)

Q37: In which 3 phase system, the artificial neutral is required to measure the phase voltage?

3 wire star connected system
4 wire star connected system
3 wire delta connected system
4 wire delta connected system

Q38: What is the line voltage in 3 phase system if the phase voltage is 240V?

380 Volt
400 Volt
415 Volt
440 Volt

Show Calculation

\[ Given: V_P = 240\,\text{V}\] \[ Line Voltage in star: V_L = \sqrt{3} \times V_P\]\[ = 1.732 \times 240 = 415.68\,\text{V} \approx 415\,\text{V}\]

Q39: Which formula is used to calculate Form factor \((K_f)\)?

\(K_f = \frac{Effective ~value}{Average ~value}\)
\(K_f = \frac{Maximum ~value}{Effective~ value}\)
\(K_f = \frac{Maximum~ value}{Average~ value}\)
\(K_f = \frac{Average ~value}{Effective ~value}\)

Q40: Which formula is used to calculate the impedance (z) of a RLC series circuit?

\(Z = R + X_L + X_C\)
\(Z = R + (X_L + X_C)\)
\(Z = R - (X_L \sim X_C)\)
\(Z = \sqrt{R^2 + (X_L \sim X_C)^2}\)

Q41: What is the power factor if one of the wattmeter gives negative reading in two wattmeter method of 3 phase power measurement?

0
0.5
Unity
Less than 0.5

Q42: What is the phase displacement between phases in a 3 phase circuit?

90°
120°
180°
360°

Q43: Which condition is called as resonance RLC circuit?

\(X_L\) > \(X_C\)
\(X_C\) > \(X_L\)
\(X_L\) = \(X_C\)
R < \(X_L\)

Q44: Which quantity is rotating at a constant angular velocity?

Scalar quantity
Vector quantity
Phasor quantity
Algebraic quantity

Found a mistake or mismatch in the question or answer? Let us know via email.

1st year, Trade Theory

Theory ITI

This post is licensed under CC BY 4.0 by the author.

Q1: What is the unit of susceptance?

Q2: What is the resistance of the inductive coil takes 5A current across 240V, 50Hz supply at 0.8 power factor?

Q3: How the resonance frequency \((f_r)\) can be increased in A.C series circuit?

Q4: What is the formula to find 3 phase Reactive power \((P_R)\) if the line voltage is \(V_L\) and line current is \(I_L\)?

Q5: What is the main cause for below 0.5 lagging power factor in 3 phase system?

Q6: What is the current in neutral conductor in 3 phase unbalanced load in star connected system?

Q7: Calculate the apparent power in KVA of 3 phase 415V, 50 Hz, star system, if the line current \((I_L)\) is 16A at 0.8 power factor.

Q8: What will be the readings of two watt meters \((W_1\) & \(W_2)\) in 3 phase power measurement, if the power factor is zero?

Q9: What is the maximum value of voltage for 240 volt RMS?

Q10: What is the condition for resonance in RLC series circuit? (Inductive reactance = \(X_L\), Capacitive reactance = \(X_C\))

Q11: What is the formula for Reactive Power \((P_r)\) in an AC circuit?

Q12: Calculate the impedance of the circuit R = 5Ω, \(X_L\)= 36Ω and \(X_C\) = 24 Ω.

Q13: What is the phase displacement in a single phase AC circuit?

Q14: What is the relation between the line voltage \((V_L)\) and phase voltage \((V_p)\) in star connected system?

Q15: Calculate the line current of the 3 phase 415V 50 HZ supply for the balanced load of 3000 watt at 0.8 power factor is connected in star.

Q16: What is the power factor in a 3 phase power measurement of two wattmeters showing equal readings?

Q17: Calculate the power factor of coil having resistance of 24Ω, draws the current of 5A, at 240V/ 50Hz AC supply.

Q18: What is the formula to calculate the impedance (Z) of the R.L.C series circuit, if the inductive reactance \((X_L)\) is less than capacitive reactance \((X_C)\)?

Q19: Calculate the power factor of R.L.C circuit having resistance (R) = 15Ω, resultant reactance (X) = 20Ω connected across 240V /50Hz AC supply?

Q20: Calculate the value admittance (Y) of the RLC parallel circuit connected across 240volts/50Hz AC supply and 8 Amp. Current is passed through it?

Q21: What is the formula to calculate the line current \((I_L)\) of this single phase R - C parallel circuit?

Q22: How the low power factor (P.F) can be improved in AC circuits?

Q23: What is the formula to calculate the three phase active power (P) if the line voltage (VL) and line current is \(I_L\) and phase angle is ‘θ’?

Q24: What is the relation between the line current \((I_L)\) and phase current \((I_P)\) in delta connected system?

Q25: What is the purpose of phase sequence meter?

Q26: Calculate the apparent power of a star connected 3 phase load, if it is connected across 3 phase 415volt/50Hz supply at 0.8 p.f and the phase current is 10 Amps.

Q27: What is the P.F if one of the wattmeters reading is zero and the other reads total power in 2 wattmeter method of 3 phase power measurement?

Q28: Which electrical term is defined as the total opposition to current in AC parallel circuit?

Q29: Which AC circuit contains the phase relation between voltage (V) and current (I)?

Q30: In a 3 phase system, if the active power is 4 kw and the apparent power is 5 KVA, calculate the reactive power?

Q31: In which condition resonance will occur in R-L-C series circuit?

Q32: How will you obtain positive reading in the wattmeter reads negative reading during 3-phase two wattmeter method?

Q33: What is the form factor \((K_f)\) for sinusoidal AC?

Q34: What is the reciprocal of inductance in AC parallel circuit?

Q35: What relationship is illustrated in between the current and voltage?

Q36: Calculate the total power by two wattmeter \((W_1\) & \(W_2)\) method, if one of the wattmeter \((W_2)\) reading is taken after reversing.

Q37: In which 3 phase system, the artificial neutral is required to measure the phase voltage?

Q38: What is the line voltage in 3 phase system if the phase voltage is 240V?

Q39: Which formula is used to calculate Form factor \((K_f)\)?

Q40: Which formula is used to calculate the impedance (z) of a RLC series circuit?

Q41: What is the power factor if one of the wattmeter gives negative reading in two wattmeter method of 3 phase power measurement?

Q42: What is the phase displacement between phases in a 3 phase circuit?

Q43: Which condition is called as resonance RLC circuit?

Q44: Which quantity is rotating at a constant angular velocity?

Trending Tags