Mensuration
Workshop Calculation and Science, Module-8
Q1: What is the area of a square whose side is 18 cm?
- 26 cm²
- 36 cm²
- 72 cm²
- 324 cm²
Show Explanation
Area of a square is:
\[ A = \text{side}^2 = 18^2 = 324\ \text{cm}^2 \]
Q2: What is the diagonal of a square plate whose side is 28 cm?
- 39.29 cm
- 39.39 cm
- 39.49 cm
- 39.59 cm
Show Explanation
Diagonal of a square is:
\[ d = a\sqrt{2} = 28 \times \sqrt{2} \approx 39.59\ \text{cm} \]
Q3: What is the side of a square whose area is 625 mm²?
- 15 mm
- 20 mm
- 25 mm
- 30 mm
Show Explanation
\[ A = a^2 \Rightarrow a = \sqrt{625} = 25\ \text{mm} \]
Q4: What is the perimeter of a rectangle whose length and breadth are 20 cm and 18 cm?
- 56 cm
- 66 cm
- 76 cm
- 86 cm
Show Explanation
Perimeter of a rectangle:
\[ P = 2(l + b) = 2(20 + 18) = 2 \times 38 = 76\ \text{cm} \]
Q5: What is the area of a rectangle, whose length and breadth are 10 cm and 8 cm respectively?
- 75 cm²
- 80 cm²
- 85 cm²
- 90 cm²
Show Explanation
Area of a rectangle:
\[ A = l \times b = 10 \times 8 = 80\ \text{cm}^2 \]
Q6: What is the formula for area of parallelogram?
- A = \(b × h\)
- A = \(\frac{1}{2} × b × h \)
- A = \(\frac{b + h}{2}\)
- A = \(\frac{1}{2} × \frac{1}{b} × h\)
Show Explanation
Area of a parallelogram is:
\[ A = b \times h \] where \(b\) is the base and \(h\) is the height.
Q7: What is the area of a right angled triangle having a base 10 cm and height 5 cm?
- 20 sq.cm
- 25 sq.cm
- 30 sq.cm
- 35 sq.cm
Show Explanation
Area of a right-angled triangle:
\[ A = \frac{1}{2} \times \text{base} \times \text{height} \]\[= \frac{1}{2} \times 10 \times 5 = 25\ \text{cm}^2 \]
Q8: What is the perimeter of scalene triangle having sides of 40 mm, 20 mm and 28 mm?
- 68 mm
- 78 mm
- 88 mm
- 98 mm
Show Explanation
Perimeter is sum of all sides:
\[ P = 40 + 20 + 28 = 88\ \text{mm} \]
Q9: What is the area of an equilateral triangle of side 450 mm?
- 856.82 cm²
- 866.82 cm²
- 876.82 cm²
- 886.82 cm²
Show Explanation
Area of an equilateral triangle:
\[ A = \frac{\sqrt{3}}{4} a^2 = \frac{\sqrt{3}}{4} \times (45)^2 = 876.82\ \text{cm}^2 \] Note: 450 mm = 45 cm
Q10: What is the area of a circle of diameter 50 cm?
- 1932.5 cm²
- 1942.5 cm²
- 1952.5 cm²
- 1962.5 cm²
Show Explanation
Radius = \(\frac{50}{2} = 25\) cm
Area of a circle:
\[ A = \pi r^2 = \pi \times 25^2 = 1962.5\ \text{cm}^2\ \]\[(\text{using } \pi \approx 3.14) \]
Q11: What is the area of a semicircle whose diameter is 20 cm?
- 147.1 cm²
- 157.1 cm²
- 167.1 cm²
- 177.1 cm²
Show Explanation
Radius = \(\frac{20}{2} = 10\) cm
Area of semicircle:
\[ A = \frac{1}{2} \pi r^2 = \frac{1}{2} \times 3.14 \times 10^2 = 157.1\ \text{cm}^2 \]
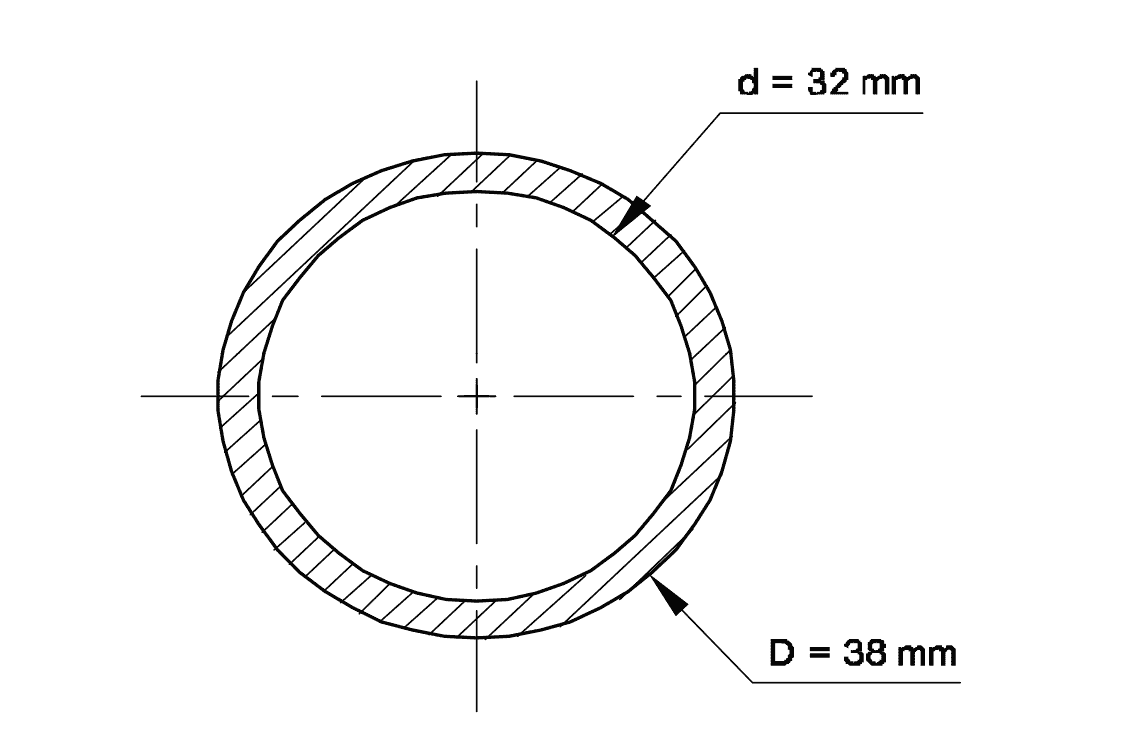
Q12: What is the cross sectional area of a circular ring of D = 38 mm and d = 32 mm?
- 320 mm²
- 330 mm²
- 340 mm²
- 350 mm²
Show Explanation
\[ A = \frac{\pi}{4} (D^2 - d^2) = \frac{3.14}{4} (38^2 - 32^2) \]\[= \frac{3.14}{4} (1444 - 1024) = \frac{3.14}{4} \times 420 \]\[= 329.85 mm² ≈ 330 mm²\]
Q13: What is the area of a sector of a circle of radius 5 cm and its angle is 96°?
- 20.39 cm²
- 20.93 cm²
- 20.89 cm²
- 20.98 cm²
Show Explanation
\[ A = \frac{\theta}{360} \pi r^2 = \frac{96}{360} \times 3.14 \times 5^2 \]\[= \frac{96}{360} \times 3.14 \times 25 \approx 20.93\ \text{cm}^2 \]
Q14: What is the formula for area and perimeter of a hexagon?
- \(\frac{3\sqrt{3}}{4} a^2\), 3a
- \(\frac{4\sqrt{3}}{4} a^2\), 4a
- \(\frac{5\sqrt{3}}{4} a^2\), 5a
- \(\frac{6\sqrt{3}}{4} a^2\), 6a
Show Explanation
Regular hexagon area and perimeter:
\[ A = \frac{3\sqrt{3}}{2} a^2 = \frac{6\sqrt{3}}{4} a^2,\quad P = 6a \]
Q15: What is the area of an ellipse if the major and minor axes are 10 cm and 6 cm respectively?
- 27 cm²
- 37 cm²
- 47 cm²
- 57 cm²
Show Explanation
Semi-major axis \(a = \frac{10}{2} = 5\), semi-minor axis \(b = \frac{6}{2} = 3\)
\[ A = \pi a b = 3.14 \times 5 \times 3 = 47.1 \approx 47\ \text{cm}^2 \]
Q16: Find the total surface area of cube whose side is 25 cm.
- 3740 cm²
- 3745 cm²
- 3750 cm²
- 3755 cm²
Show Explanation
Total surface area of cube:
\[ A = 6a^2 = 6 \times 25^2 = 6 \times 625 = 3750\ \text{cm}^2 \]
Q17: Find the total surface area of a cast iron bar whose length, width and height are 20 m, 15 m and 12 m.
- 1340 m²
- 1440 m²
- 1540 m²
- 1640 m²
Show Explanation
Total surface area of cuboid:
\[ A = 2(lw + lh + wh) \]\[= 2(20\times15 + 20\times12 + 15\times12) \]\[= 2(300 + 240 + 180) = 2 \times 720 = 1440\ \text{m}^2 \]
Q18: What is the formula for total surface area of a cylinder?
- \(2\pi r(h + r)\) unit²
- \(\pi r(h + r)\) unit²
- \(\pi r h\) unit²
- \(2\pi r h\) unit²
Show Explanation
Total surface area of a cylinder:
\[ A = 2\pi r(h + r) \] where \(r\) is the radius and \(h\) is the height.
Q19: What is the volume of a rectangular tank of 30 m length, 20 m width and 10 m height?
- 5900 m³
- 6000 m³
- 6100 m³
- 6200 m³
Show Explanation
Volume of a cuboid (tank):
\[ V = l \times w \times h = 30 \times 20 \times 10 = 6000\ \text{m}^3 \]
Q20: What is volume of the cylinder whose radius is 7 cm and height 12 cm?
- 1842 c.c
- 1844 c.c
- 1846 c.c
- 1848 c.c
Show Explanation
Volume of cylinder:
\[ V = \pi r^2 h = 3.14 \times 7^2 \times 12 \]\[= 3.14 \times 49 \times 12 = 1845.36 \approx 1846\ \text{cm}^3 \]
Q21: What is the volume of sphere of radius 7 cm?
- 1436 cm3
- 1463 cm3
- 1346 cm3
- 1636 cm3
Show Explanation
\[ V = \frac{4}{3} \pi r^3 = \frac{4}{3} \times 3.14 \times 7^3 \]\[= \frac{4}{3} \times 3.14 \times 343 \approx 1436\ \text{cm}^3 \]
Q22: What is the formula for finding volume of a hollow cylinder having outer radius 'R' inner radius 'r' and height 'h'?
- \(\pi (R^2 - r^2) h\) unit3
- \(\frac{\pi}{3} (R^2 - r^2) h\) unit3
- \(\frac{2}{3} \pi (R^2 - r^2) h\) unit3
- \(\frac{4}{3} \pi (R^2 - r^2) h\) unit3
Show Explanation
\[ V = \pi (R^2 - r^2) h \] where \(R\) is outer radius, \(r\) is inner radius, and \(h\) is height.
Q23: What is the capacity of a conical tank of radius 2 m and height 5m?
- 11 m3
- 21 m3
- 31 m3
- 41 m3
Show Explanation
\[ V = \frac{1}{3} \pi r^2 h = \frac{1}{3} \times 3.14 \times 2^2 \times 5 \]\[= \frac{1}{3} \times 3.14 \times 4 \times 5 = 20.93\ \text{m}^3 \approx 21\ \text{m}^3 \]
Q24: How many liters of water a cylindrical tank of radius 75 cm and height 100 cm can hold?
- 1766.25 liters
- 1767.25 liters
- 1768.25 liters
- 1769.25 liters
Show Explanation
\[ V = \pi r^2 h \]\[= 3.14 \times 75^2 \times 100 = 3.14 \times 5625 \times 100 \]\[= 1766250\ \text{cm}^3 = 1766.25\ \text{liters} \]
Q25: What is the total surface area of a cylinder having radius 2 metres and height 5 metres?
- 86 sq.metre
- 88 sq.metre
- 90 sq.metre
- 92 sq.metre
Show Explanation
\[ \text{TSA} = 2\pi r (r + h) = 2 \times 3.14 \times 2 \times (2 + 5) \]\[= 2 \times 3.14 \times 2 \times 7 = 88\ \text{m}^2 \]
Q26: Find the curved surface area of a cylinder 10 cm dia and 20 cm height?
- 620 cm2
- 628 cm2
- 630 cm2
- 638 cm2
Show Explanation
Radius = \(\frac{10}{2} = 5\ \text{cm}\)
Curved Surface Area (CSA) of cylinder:
\[ \text{CSA} = 2\pi r h = 2 \times 3.14 \times 5 \times 20 = 628\ \text{cm}^2 \]