Trigonometry
Workshop Calculation and Science, Module-10
Q1: How many degrees is equal to one radian?
- 360/π°
- π/360°
- π/180°
- 180°/π
Q2: Which is equal to sinθ?
- Opposite side / Hypotenuse
- Hypotenuse / Opposite side
- Adjacent side / Hypotenuse
- Hypotenuse / Adjacent side
Q3: What is equal to cosθ?
- Hypotenuse / Adjacent side
- Adjacent side / Hypotenuse
- Opposite side / Hypotenuse
- Hypotenuse / Opposite side
Q4: What is equal to tanθ?
- Opposite side / Hypotenuse
- Adjacent side / Hypotenuse
- Opposite side / Adjacent side
- Adjacent side / Opposite side
Q5: What is the value of tanθ if sinθ = 4/5?
- 3/4
- 4/5
- 3/5
- 4/3
Show Explanation
Given: \[\sin \theta = \frac{4}{5}\]
Use identity: \(\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}}\) ⇒ Opposite = 4, Hypotenuse = 5
Find Adjacent side using Pythagoras:
\[ \text{Adjacent} = \sqrt{5^2 - 4^2} = \sqrt{25 - 16} = \sqrt{9} = 3 \] \[ \tan \theta = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{4}{3} \]
Q6: What is the value of θ if sinθ = √3/2?
- 30°
- 45°
- 60°
- 90°
Show Explanation
From trigonometric table:
\[ \sin 60^\circ = \frac{\sqrt{3}}{2} \] Hence, \(\theta = 60^\circ\)
Q7: What is the value of tan 45° if sin 45° = 1/√2?
- 1
- 1/2
- √3
- √2
Show Explanation
Given: \(\sin 45^\circ = \frac{1}{\sqrt{2}}\)
We know from standard trigonometric values: \[ \tan 45^\circ = \frac{\sin 45^\circ}{\cos 45^\circ} = \frac{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}} = 1 \]
Q8: What is the value of sin 30° if cos 30° = √3/2?
- 2/3
- 1/2
- √3/2
- 1/√2
Show Explanation
Given: \(\cos 30^\circ = \frac{\sqrt{3}}{2}\)
From standard trigonometric identities: \[ \sin 30^\circ = \frac{1}{2} \]
Q9: What is 1 + cot²θ?
- sec²θ
- cosec²θ
- cot²θ
- tan²θ
Q10: What is the height of the wall where the ladder touches the wall if the ladder is 2.5 m long makes an angle of 60° with the ground?
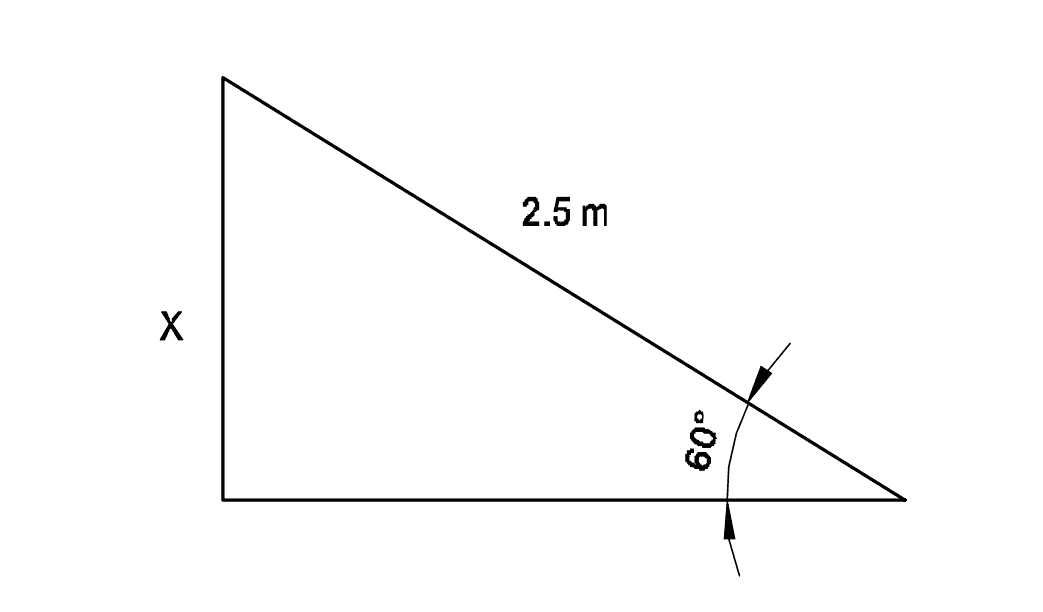
- 4.13 m
- 4.23 m
- 4.33 m
- 4.43 m
Show Explanation
Use: \(\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}}\)
\[ \sin 60^\circ = \frac{h}{2.5} \Rightarrow \frac{\sqrt{3}}{2} = \frac{h}{2.5}\]\[ \Rightarrow h = \frac{\sqrt{3}}{2} \times 2.5 \approx 4.33\ \text{m} \]
Q11: What is the height of AC?
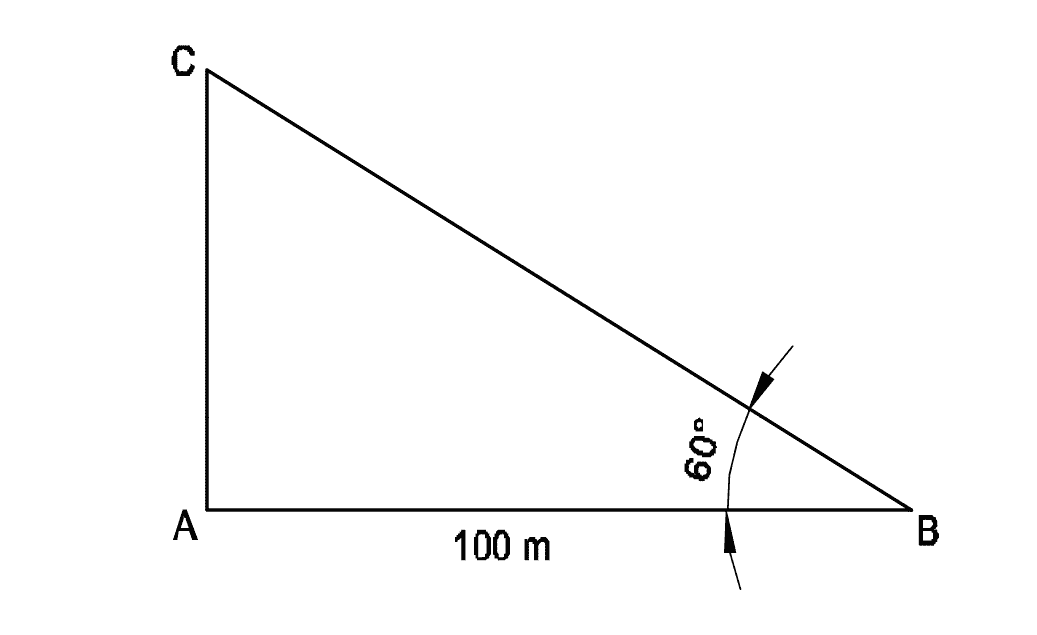
- 1.732 m
- 17.32 m
- 173.2 m
- 1732 m
Show Explanation
If AC = \(100 \times \sqrt{3} \Rightarrow 100 \times 1.732 = 173.2\ \text{m}\)
This is a typical trigonometry setup where tan or sin is used with √3.
Q12: What is the height of the building if a ladder at 45° touches the building placed 16 m from the base of the building?
- 15 m
- 16 m
- 17 m
- 18 m
Show Explanation
\[ \tan 45^\circ = \frac{\text{height}}{16} = 1 \Rightarrow \text{height} = 16\ \text{m} \]
Q13: What is the angle of elevation of the top of a light house of 15 m height seen at a point 15 m away from the base?
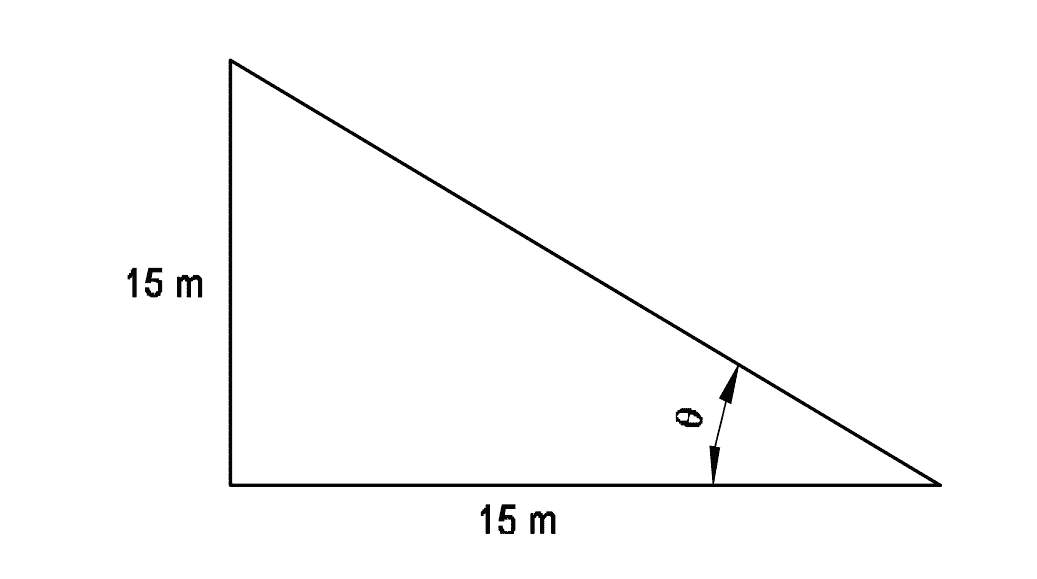
- 30°
- 45°
- 60°
- 90°
Show Explanation
If height = base = 15 m, then:
\[ \tan \theta = \frac{15}{15} = 1 \Rightarrow \theta = 45^\circ \]
Q14: What is the angle of θ?
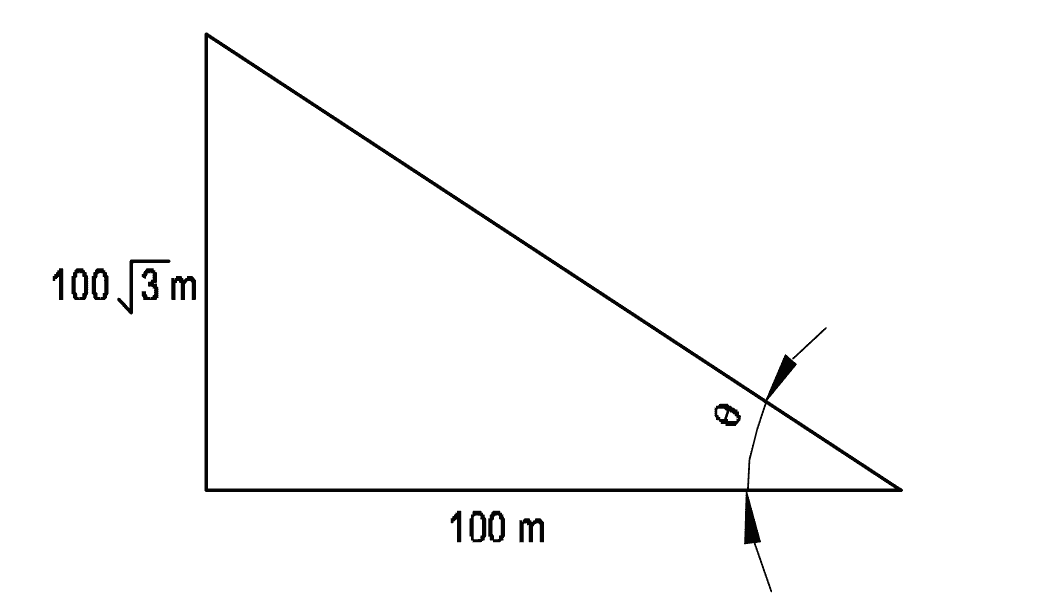
- 30°
- 45°
- 60°
- 90°
Show Explanation
Given:
Opposite = \(100\sqrt{3}\) m, Adjacent = \(100\) m
Use: \[ \tan \theta = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{100\sqrt{3}}{100} = \sqrt{3} \] From standard trigonometric ratios: \[ \tan 60^\circ = \sqrt{3} \Rightarrow \theta = 60^\circ \]
Q15: What is the term for the object seen higher than eye level?
- Angle of inclination
- Angle of friction
- Angle of elevation
- Angle of depression
